racecar仿真竞赛经验总结（七）- Pure pursuit纯追踪算法

前文链接：

racecar仿真竞赛经验总结（一） - 前言

racecar仿真竞赛经验总结（二）- racecar仿真模型介绍

racecar仿真竞赛经验总结（三）- 激光SLAM建图

racecar仿真竞赛经验总结（四）- AMCL与小车定位

racecar仿真竞赛经验总结（五）- TF树

racecar仿真竞赛经验总结（六）- Navigation导航包

博文推荐

原理部分推荐博文：

知乎：https://zhuanlan.zhihu.com/p/48117381

CSDN：https://blog.csdn.net/gophae/article/details/100012763

Github源码参考链接：

https://github.com/jmaye/pure-pursuit-controller-ros

https://github.com/Hypha-ROS/hypharos_racecar

https://github.com/leggedrobotics/se2_navigation

原理简述

车辆轨迹跟踪，目前的主流方法分为两类：基于几何追踪的方法和基于模型预测的方法。本文主要介绍基于几何追踪的pure-pursuit（纯跟踪）算法。

阿克曼转向几何

首先介绍一下车辆的转向模型–阿克曼转向几何

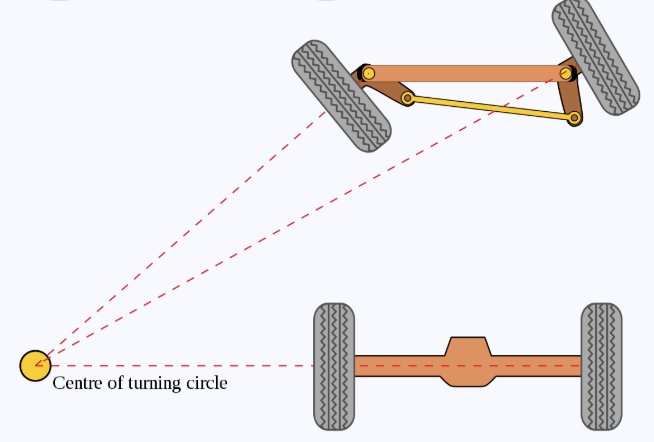
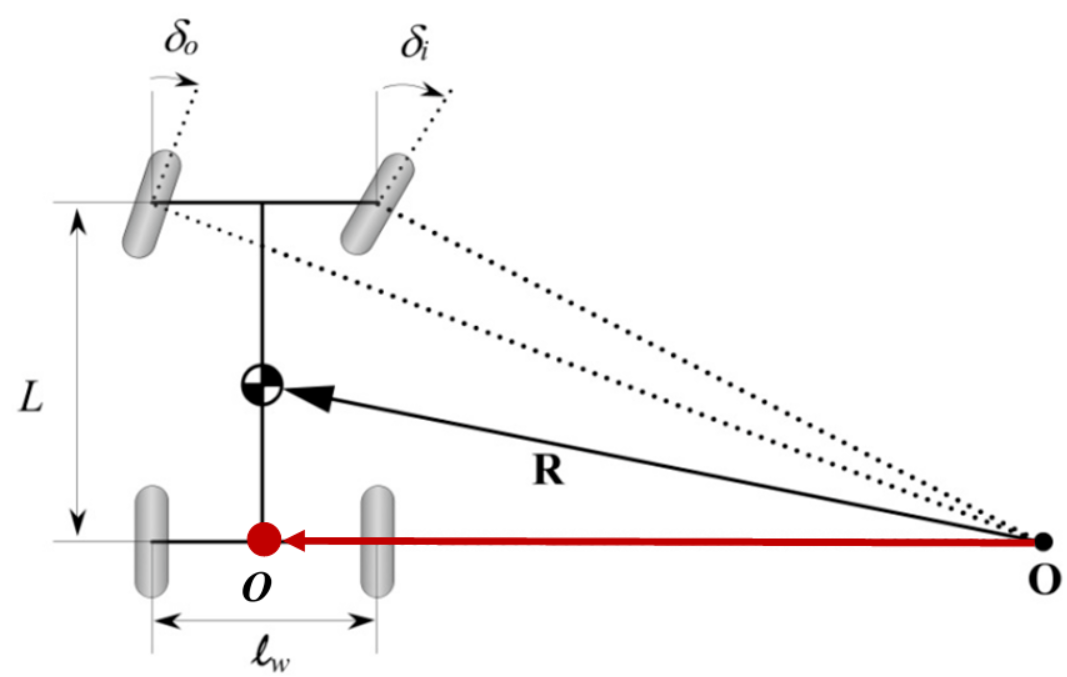
对转向时（假定小转向角）的正确几何关系，由于内外侧轮胎的转向半径不同，可以得出左右轮转向角为：

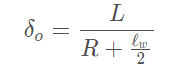
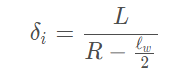
则前轮平均转角为：

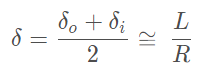
自行车模型

接下来，我们再来看一个阿克曼几何的简化版–车辆单轨模型（即自行车模型）

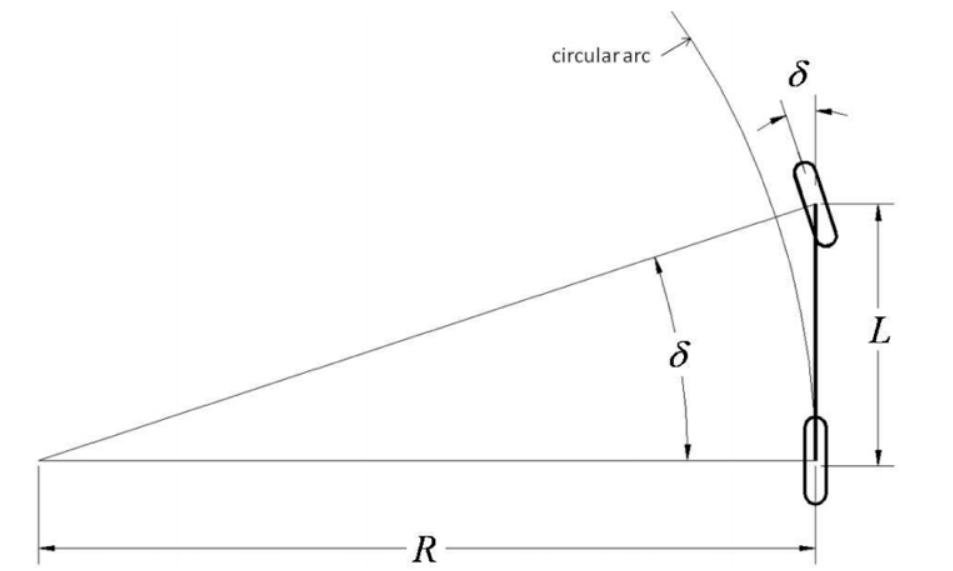
自行车模型实际上是对阿克曼转向几何的一个简化，我们知道，自行车模型将4轮车辆简化成2轮的模型，并且假定车龄只在平面上行驶，采用自行车模型的一大好处就在于它简化了前轮转向角与后轴将遵循的曲率之间的几何关系，其关系如下式所示：

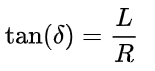
其中δ表示前轮的转角，L为轴距（Wheelbase），R则为在给定的转向角下后轴遵循着的圆的半径。这个公式能够在较低速度的场景下对车辆运动做估计。

Pure pursuit纯追踪算法

从自行车模型出发，纯跟踪算法以车后轴为切点, 车辆纵向车身为切线, 通过控制前轮转角，使车辆可以沿着一条经过目标路点（goal point）的圆弧行驶，如下图所示：

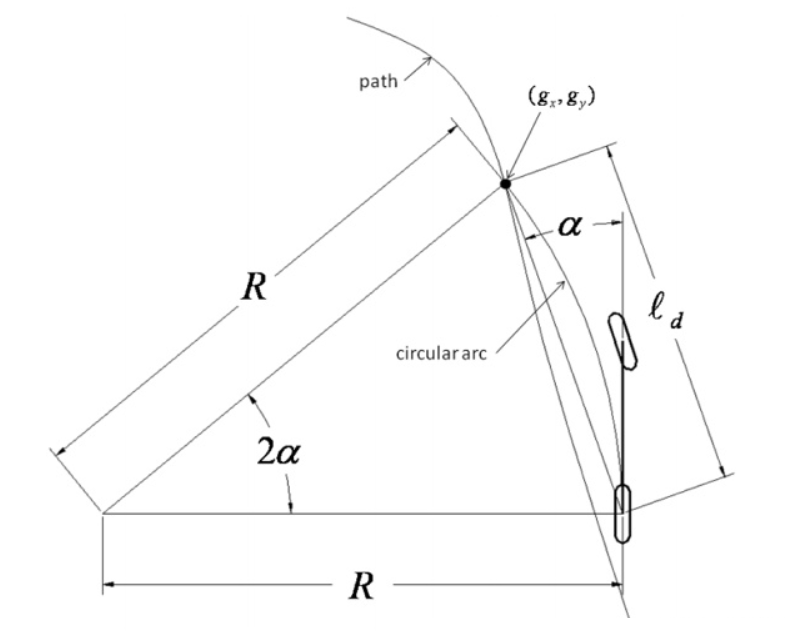
如上，pure pursuit 需要给出预瞄距离Ld，因此后期当工作效果不好的时候可以对这个预瞄距离进行tuning，但是过程繁琐，在某些情况下使用该模型效果不佳。给定预瞄距离后在预定轨迹上获得采样点(gx,gy)。本车的后轴中心，采样点(gx,gy)，以及车辆的运动学半径中心行程三角形，根据sin正弦函数三角公式，获得如下：

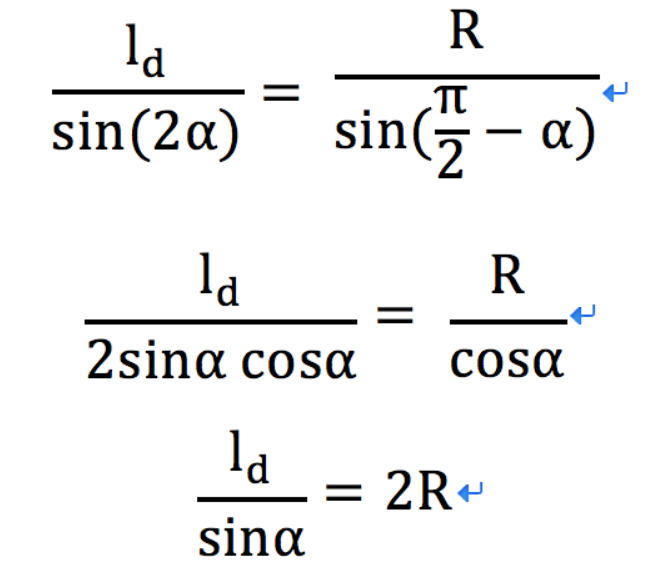
因为道路的曲率：

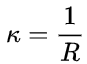
上式也可以表示为：

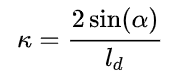
则由自行车模型中的式子 ，可得

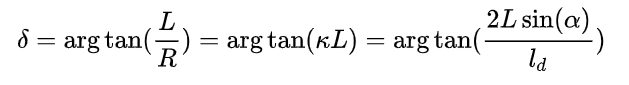
改进部分

引入横向偏差

我们知道pure pursuit中的控制方法只对角度进行了控制，这种方法在实践中会出现一个弊端，纯在某种情况——小车的角度已经符合要求但并不在所规划的路线上，而是与其平行。我们的改进方法之一就是添加横向偏差，令其自动纠正这种平行的现象

由于原理相同但实现方法很多，这里引用 博客链接 中的描述——Stanley进行描述

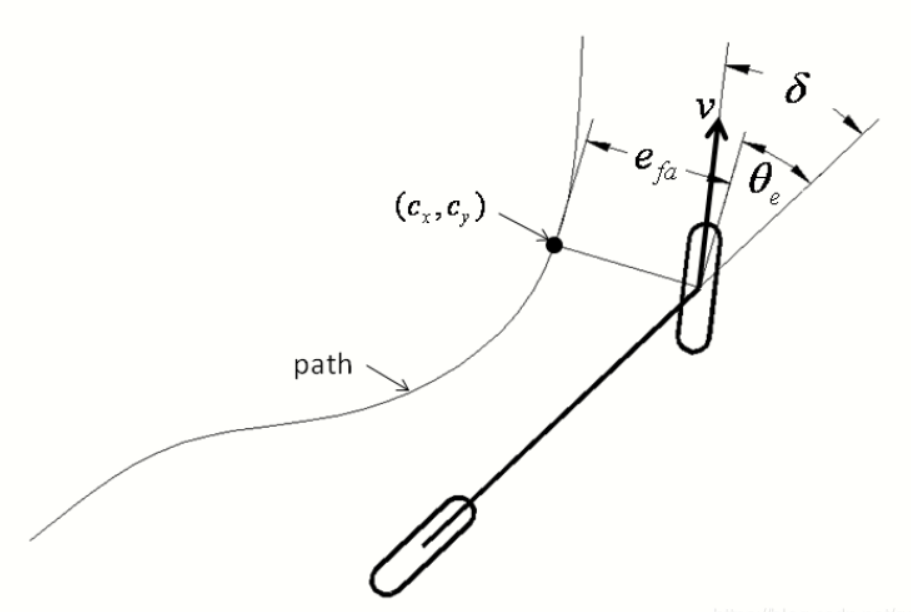
Stanley 考虑到了车辆后轴中心与预定轨迹的横向偏差e_fa，车辆头指向与预定轨迹heading angle 方向的夹角，stanley车辆期望转角的第一项为

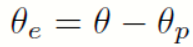
这里，theta为车辆的真实heading angle，theta_p为预定轨迹点的heading angle，差值就是车辆需要被纠正的heading angle。如果横向偏差不为零，车辆期望转角会产生第二个控制量，这个控制量和pure pursuit很相似，由前轴中心对应的车辆预定轨迹点C出，往切线防线延伸预瞄距离L，这里的预瞄距离仍然与车速成正比。于是，两项控制量可合并为：

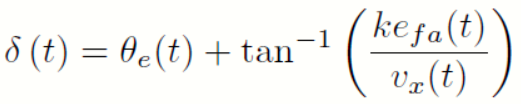
体现在源码上如下：

angle_error = self.determine_steering_angle(self.Pose, self.NextPoint)
angle = angle_raw + 0.2215*angle_error

# ...

def determine_steering_angle(self, pose, lookahead_point):
        global steering_angle_last
        rot = np.matrix([[np.cos(-pose[2]), -np.sin(-pose[2])], [np.sin(-pose[2]), np.cos(-pose[2])]]) # [ [a,b] , [c,d] ]
        delta = np.matrix([[lookahead_point[0] - pose[0]],[lookahead_point[1] - pose[1]]])
        local_delta = (rot*delta).transpose()
        local_delta = np.array([local_delta[0,0], local_delta[0,1]])
        angle_error = self.model.steering_angle(local_delta)
        return angle_error

引入前馈控制

这一块内容是为了给小车一个预先量，防止小车高速过程中无法及时调整其角度和速度

我们知道阿卡曼模型的小车无论是用TEB和DWA等局部路径规划还是使用纯追踪算法都是需要解算出小车的角度及速度，再发布给小车控制器达到控制小车的目的，而当小车速度达到一定程度时可能会出现控制器输出的角度、速度无法实现及时且精准的控制

博主是用的纯追踪算法框架，其核心就是追踪路径规划算法规划出的全局/局部路径，而路径是以若干个点为元素的数组，我们的做法简单概括就是取包括小车下一目标点在内的多个点一同作为小车angle和velocity输出，在思想上类似于引入前馈控制

体现在源码上就是

#Calculate the angle to control
angle_to_go = []
if goal>=(len(dist_array)-3):
	Ls = dist_array[goal]
	diff_angles = path_points_w[goal] - yaw # Find the turning angle
	rs = Ls/(2*math.sin(diff_angles)) # Calculate the turning radius
	angle_raw = math.atan(0.335/rs) # Find the wheel turning radius
else:
	for i in range(0,3):
		Ls = dist_array[goal+i]
		diff_angles = path_points_w[goal+i] - yaw # Find the turning angle
		rs = Ls/(2*math.sin(diff_angles)) # Calculate the turning radius
		angles = math.atan(0.335/rs) # Find the wheel turning radius
		angle_to_go.append(angles)
	angle_raw = 0.5*angle_to_go[0] + 0.3*angle_to_go[1] + 0.2*angle_to_go[2]

# ...

#Calculate the velocity to control
diff_control_angle_array = []
# ponits after goal
for i in range(0,3):
	veclocity_control = self.dist((path_points_x[goal+i], path_points_y[goal+i]), (x,y))
	control_L = dist_array[goal+i]
	diff_control_angle = path_points_w[goal+i] - yaw # Find the turning angle
	control_r = control_L/(2*math.sin(diff_control_angle)) # Calculate the turning radius
	control_angle = math.atan(0.335/control_r) # Find the wheel turning radius
	diff_control_angle_array.append(control_angle)
angle_control = np.mean(diff_control_angle_array)